Updated: October 23, 2009
A few days ago, I was sitting, thinking about a reality show that I'd like to produce. It would be called Inane or Futile or Sisyphic or something along those lines and the whole point would be to make the participants try to do the impossible, sort of a humiliation without success. Then I had the epiphany. Forcing people to do things they perceive as impossible is one thing, forcing them to do something they think they can achieve when it's utterly hopeless is another. It's called PhD in sadism. The result: swimming in honey.
This was the masterpiece I was talking about. A reality show where contestants would be immersed in honey and made to swim from one end of a pool to another. They would be wearing swimming suits and breathing apparati and all, but the whole point is, they would be submerged entirely. Can it be done? Well, here's another lesson in Hillbilly physics ...

Swimming in honey
To fully understand the scope of the problem at hand, I must spend a few minutes and educate you on liquid dynamics. Fluids have all kinds of properties, including density and viscosity. Viscosity and density are two different things, although the average guy will have a hard time telling which is which. For example, the air and water have near identical viscosity. What? Yup. However, the air has a much lesser density.
Density is what you instinctively think of - how much of the stuff is crammed into this or that unit of volume. Viscosity, on the other hand, tells us how strongly the fluid resists deformation to stress. The higher it is, the more resistant the fluid is. Just like water and honey. Stirring a spoon in water is easier than doing that in honey, right. This is because honey does not like to be stirred.
Types of flow
There are two types of flow - laminar and turbulent. A laminar flow is one where predicting the location of a particle within the flow down the trouser of time is possible. A turbulent flow is one where predicting the location of a particle within the flow over time is not possible.
You can perform a little experiment of your own: turn the tap on and let the water flow. First, open the tap gently and let the water flow at a low speed. You will notice the flow is smooth, the water transparent and the body of water oozing from the tap maintains the cylindrical shape of the pipe it just poured out. If you turn the tap on fully, the water will gush out in a turbulent squirt, turning white as it mixes with air bubbles and squirting all over the place.
Which one is better?
Now, which one do you think is more beneficial for transport - laminar flow or turbulent flow? Contrary to intuition, it's the turbulent flow you will prefer. We will soon learn why. But let me give you just a few examples:
Golf ball
Have you noticed the golf balls are dimpled? The reason for this is: make the air flow around the ball turbulent, thus reducing the drag and increasing the distances the ball can travel. It's all about this thingie called boundary layer and Magnus lift. The dimples aid the rapid formation of a turbulent boundary layer around the golf ball in flight, giving more lift. Here's a nice article on the subject: Why are Golf Balls Dimpled?

Aircraft
Have you noticed aircraft have all sorts of tiny notches on their wings? Again, the reason for this is similar to the golf ball syndrome. You want the air flowing around the wings to follow the surface of the wings. A turbulent flow can follow the surface much more easily than the laminar one, thus increasing lift and reducing drag.

Back to our problem
Yes, now we know that the turbulent flow is good for us. It allows energy/momentum to be transported more efficiently. Now, let's see what our reality TV swimmer would have to face. Let's assume it's a he (man).
He would be placed in a container that is roughly equivalent to a pipe with a rectangular cross-section. The swimmer would try to exert forward motion by flapping his hands and legs. If the viscosity, density of the fluid and the speed of swimmer's motions were such that they did not permit a turbulent flow, our man would be stuck in place.
He would affect a disturbance in the medium, in the form of eddies. For those who wonder what eddies are, these are non-capitalized nicknames for Edward. Seriously, eddies are small currents at a variance with the main stream. These eddies would be canceled out by momentum gradients caused by molecular viscosity.
Now, if our swimmer could create a turbulence, he would create eddies that have a viscosity, called eddy viscosity, that is several orders of magnitude higher than the molecular viscosity of the fluid. The eddies would be able to transport the swimmer's energy before it got canceled out, all the way to the edge of the pipe, in our case a honey-filled pool, creating a forward motion.
In purely mathematical terms, laminar motion is like a dampened harmonic oscillator. Turbulent motion is about exponents going wild and growing. Once the motion becomes non-linear, it's chaos all the way. But chaos makes for much better transport of energy (information), which explains why bad news travel so fast.
On average, traveling in a turbulent flow, you will manage a much higher, more uniform velocity profile over time than in a laminar flow. As crazy as it sounds, it's physics. The one question remains is: We know the viscosity and density of honey. We just need to know the speed that our swimmer requires to best the honey into turbulence.
The Reynold's number
The magic word here is: the Reynold's number. This number defines when whether our flow is going to be laminar or turbulent. The threshold is at around 2300. In other words, if the Reynolds number of our flow exceeds this figure, it's likely to be a turbulent one. The Reynold number takes into account the speed, the diameter of the "pipe", viscosity and density. The actual formula is like this:
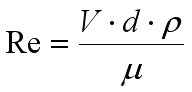
Where V is the velocity, d is the diameter, Á is the density, and ¼ is the viscosity. It is possible to make the calculation somewhat more friendly, by using kinematic viscosity, which is your normal viscosity divided by density. Honey has the kinematic viscosity of about 10-3 m2/s. Just for comparison, the kinematic viscosity of water is about 10-6 m2/s, full three orders of magnitude less. Our formula takes the following shape:
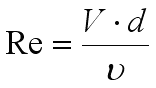
Where Å is the kinematic viscosity.
Now, we want the Reynolds number of about 2300, the swimming pool is about 5 meters wide and we have our kinematic viscosity. What we need is the velocity.
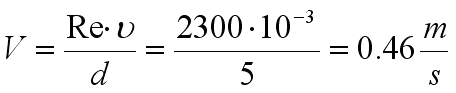
So, the speed we need is: 0.46 m/s.
That's it. Ah, seems like too little? Read on ...
Our swimmers needs to be able to move his arms and legs at the speed exceeding ~ 0.5m/s to be able create a turbulent flow and swim. Just for comparison, in water, he would need 1,000 less than that, which explains why we swim so well in water.
Can this be done?
What amount of power is required from our swimmer to manage this? Well, it's a simple deal really. Our swimmer needs to displace approx. his own weight in honey, or roughly 80kg for an average adult male, not counting the scuba equipment. In fluids, the power is a product of pressure and flow.
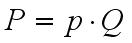
The pressure that our swimmer applies is the force (weight) of his entire body divided by the area of his swimming units, which are his palms and feet. My estimation shows that two hands and two feet have the combined surface of about 800 cm2 or 0.08 m2. This means the pressure our swimmer applies is: 800N/0.08m2 = 10,000 Pa. The flow we need is 0.5 m/s.
Thus, the power we need is roughly 5,000W or 5KW, at the very least, sustained over time. The average human body cannot produce 5KW of power. In comparison, in water, we would just need about 5W per stroke, due to viscosity being 1,000 times less. For a full hour of swimming, with one stroke taken every 5 seconds or so, we would need 1 Wh or roughly 850 cal, which is not far from the average estimation to how much energy you burn when swimming (~750). I have ignored the head and shoulders [sic] cross-section, which also take some of the pressure away, but add drag, which I have ignored. Overall, it's a good approximation. Therefore, our human cannot manage the velocity required to create a turbulent flow - and therefore, he cannot swim in honey. Lovely, eh? Damn, I'm a genius!
Conclusion
I'm the devil. My idea for the honey-swimming reality show would be a blast. People would try to achieve the unachievable, all the while I gloated about the low morality of the human society and the greed-driven need to debase oneself just for a moment of glory on the TV screens or a few zloty in the pocket. That's all for now. See ya around. If you have wicked ideas for the Hillbilly physics section, feel free to email me.
For more cool reading, see this article on Wikipedia.
Cheers.