Updated: March 4, 2013
I got massively interested in the Collatz conjecture after reading a splendid cartoon on xkcd.com, and since, I've not stopped thinking where and how it might be applied, or where and how it might manifest. As is often the case with mathematical problems, they are usually a palpable representation of a greater physical problem. And we often get to solve them through indirect experiments rather than direct observation and interaction.
So I was mulling what could intrinsically combine the fine structure constant, Pi number and other merry fellows, and I realized that the Collatz conjecture might be the one perfect candidate. What more, it comes to life all around us daily, without us ever noticing. Which is only understandable, as our discoveries are a representation, an abstraction of what and who we are. Just as CPU is a model of our brains, so is the Collatz conjecture a model of our search algorithm, in our brain. Do read.
Internet
The reason why no one saw this before is twofold: a) I'm a genius b) the Internet and tabbed browsers have been around for a fairly short period of time, preventing the critical mass discovery. But since Firefox and friends came along, offering a limitless number of open tabs, we started using the full extent of our brain search algorithm in real-life applications.
How do you go about searching for data?
Ah, there we go. First, you open some web page somewhere. Usually, it's a link-rich page, pointing to many other resources and references. The best example is a typical wiki-style web page, with important information linked to additional pages. And this is where the Collatz conjecture begins. I claim thusly:
For every page you open, you normally open two or three tabs. You always begin with one tab, so our conjecture starts with an odd member. Then, you read some and usually close one or two, then something grabs your attention and you click open a few more links. You do not do this mathematically, as the rule states, but you do this naturally, as your brain dictates. You also spend time reading, perusing information, skipping boring bits, looking at pictures of naked women, and this is when your clicks increase. Anyhow, ahem. Yes.
You begin to branch out, and your tree grows, in Collatz-like bursts, and once you exhaust the search of a given branch, you collapse it, going back down another branch. You will notice that you often veer far away from the original topic you started with. You might read on steel, and end up reading how ships are made, then venture in the history of naval battles in WWII, before going back to the manufacturing process of iron.
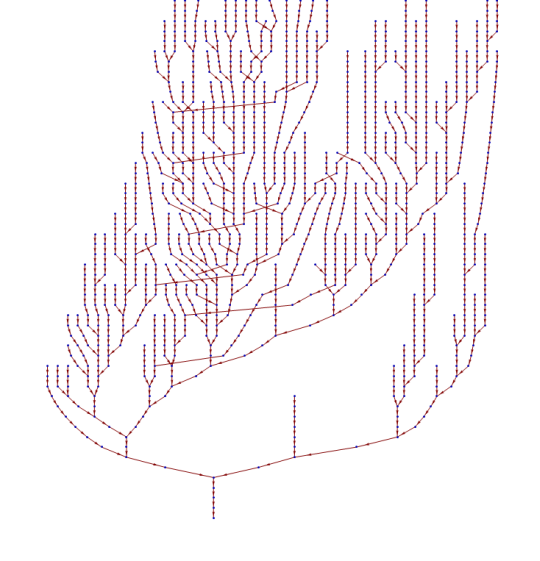
Note: Image taken and adapted from Wikipedia, courtesy of Jon McLoone.
In the end, you collapse tabs, slowly, you narrow down your search, and you finish with a single tab, usually, at the same page you started. And thus you complete a full loop of the Collatz conjecture and make nature obey its hidden laws. Of course, if you are bored, you can count your stopping times. Damn, that's bloody genius, isn't it?
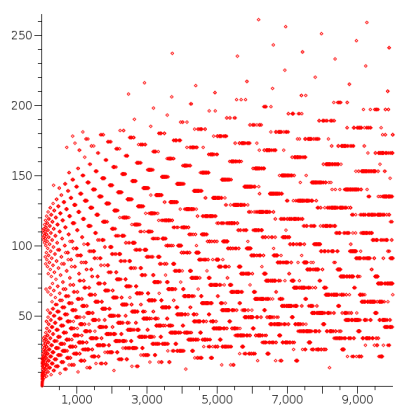
Now, it's also possible to calculate the theoretical limit of all information you can read, as well as the theoretical limit of the Internet information propagation using the conjecture. If we count the stopping times, we see that for certain numbers of search paths, i.e. tabs or vectors of information in our case, which could be hyperlinks of interest in a single webpage, the information explodes, and in other cases, it does not.
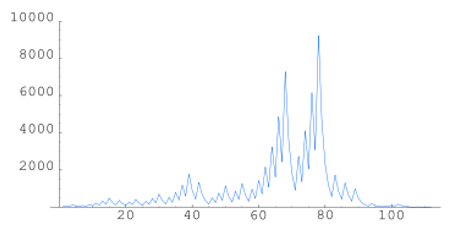
I wonder if search engines use the Collatz conjecture to award and penalize sites, and if robots use any similar algorithms. Well, now after this article gets published, they surely will. Yes, I am that amazing. But it seems for anything with 60-90 links, this is the optimal way to get your stuff out, over many thousands of hops. Perhaps this is the reason why Google recommends less than 200 hyperlinks on your pages?
Why is this?
Now comes the tricky part. Why? Well, I was trying to think what other situations might be out there that could cause our thought process to branch out. And another silly idea hit me. Real-time strategies. Let me illustrate a typical scenario. At the beginning of any which map level, you promise to take it easy and maintain full control of your units. But 40 minutes into the game, it's chaos, and you no longer have the ability to govern your seven hundred peons, orcs, tanks, or whatever it is you're building all over the map. So you scale down, neglect most of your troops, and focus on quality until the next critical moment your attention explodes due to over-management.
Apparently, our brain is not binary. We do not make decisions in the black & white mode. Our thought process is not linear either, although we do like to make linear approximations. Exponential, surely not. The nearest natural process I could think of is the Collatz conjecture. And the real-time strategy translates into real business models all around us. The conjecture defines the optimal and maximal information exchange patterns based on the number of elements involved. This model also defines the smallest - or largest - hive of information holders, or human participants if you will, that can effectively manage its information. Which is why companies beyond a few hundred people lose the information cohesion.

And then it all makes sense. It also explains why the problem has no real practical solution, i.e. no return to the initial state but an endless expansion, because there is an endless expansion to human information search, hence the mathematical model that represents our brain functionality is likewise bound, or rather, not.
Conclusion
I am absolutely certain you did not think of this. No you did not. And you are probably wondering now, whether I am an utter genius or an utter moron. But it does make sense. Can you think of a more logical, natural process of searching for information that is designed for the human brain? I cannot. Binary searches are efficient and useful and all that, but only if you are a deterministic machine with written algorithms. For humans, who can alter their thinking on the go, the Collatz search seems the most efficient and natural way of finding information.
There's some philosophy in my claim, and I am certain that if you were to randomly check a hundred people, you would find different, varying patterns of search, including single-tab serial search, very broad or very narrow trees, and anything in between. Which is fine, since people differ in intelligence, and some kind of dampening factor could also apply. But the optimal one, which takes you everywhere, seems to be the Collatz conjecture. Damn, this sounds awesome, even if it might be total bollocks. Well, I guess that would be all for today.
Cheers.